tea算法是逆向中经常遇到的一种算法
算法特征
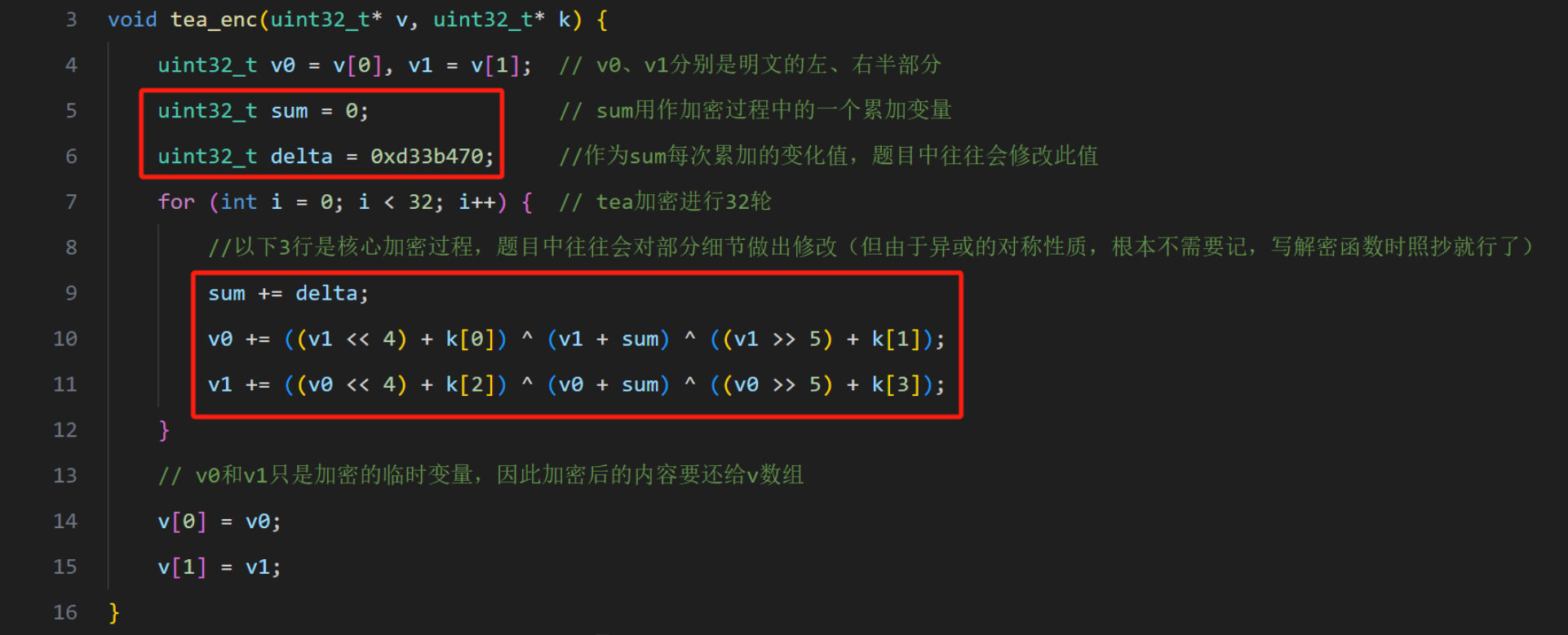
tea算法的主要特征表现在sum和delta变量,以及3行核心加密中出现的右移4左移5,两行各有3个小括号互相异或
delta的值一般为0x9E3779B9(-0x61C88647),但题目中往往会改变它的值
算法加密
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
void tea_enc(uint32_t* v, uint32_t* k) {
uint32_t v0 = v[0], v1 = v[1];
uint32_t sum = 0;
uint32_t delta = 0xd33b470;
for (int i = 0; i < 32; i++) {
sum += delta;
v0 += ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);
v1 += ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);
}
v[0] = v0;
v[1] = v1;
}
————————————————
版权声明:本文为CSDN博主「晴友读钟」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https:
|
算法解密脚本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void tea_dec(uint32_t* v, uint32_t* k) {
uint32_t v0 = v[0], v1 = v[1];
uint32_t delta = 0xd33b470;
uint32_t sum = 32 * delta;
for (int i = 0; i < 32; i++) {
v1 -= ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);
v0 -= ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);
sum -= delta;
}
v[0] = v0;
v[1] = v1;
}
|
重点抓准——无论明文是什么形式、有多长,解密时一定是每次传入两个uint32_t(32位无符号整数)

